Usa la calculadora odds ratio como un experto

Una calculadora de odds ratio es, en esencia, una herramienta para medir la fuerza con la que dos cosas están conectadas. Compara las probabilidades de que algo suceda en un grupo frente a otro y te da una respuesta clara y numérica. Es como un atajo para saber si un nuevo anuncio de verdad hace que la gente compre más o si un determinado hábito afecta a la salud.

Entendiendo el odds ratio sin complicaciones

Aunque "odds ratio" (OR) suene a jerga de estadístico, la idea es bastante intuitiva. Piénsalo como una balanza que compara dos escenarios. En un platillo pones las "odds" (las probabilidades) de que algo ocurra en un grupo que ha estado expuesto a un factor concreto. En el otro, las "odds" de que eso mismo pase en un grupo que no ha estado expuesto.

El resultado es un solo número que te cuenta una historia muy clara. Ojo, no mide la probabilidad de que algo pase, sino que compara las probabilidades relativas entre esos dos grupos. Esta diferencia es fundamental y es lo que lo convierte en una medida de asociación tan potente. En el mundo de las apuestas, por ejemplo, entender estas conexiones es clave, como ya contamos en nuestro artículo sobre cómo usar un calculador de probabilidades para ganar apuestas.

Los tres posibles resultados del odds ratio

La verdadera magia del OR es lo fácil que se interpreta. Todo se reduce a cómo se compara el resultado con el número 1.

OR > 1 (Mayor que 1): Significa que hay una asociación positiva. El grupo expuesto tiene más probabilidades de que le ocurra el evento. Si el OR es de 3, las odds son tres veces mayores en ese grupo.
OR = 1 (Igual a 1): Aquí no hay ninguna asociación. Estar expuesto al factor no influye en nada; ambos grupos tienen exactamente las mismas odds.
OR < 1 (Menor que 1): Esto indica una asociación negativa, lo que a veces se llama un "efecto protector". El grupo expuesto tiene menos probabilidades de que le suceda el evento. Un OR de 0,4 significa que sus odds son un 60 % menores.

El odds ratio no te dice por qué existe una relación, simplemente te dice lo fuerte que es. Es una pista crucial que sirve de punto de partida para investigar más a fondo, ya sea en medicina o en marketing.

Un ejemplo del mundo real

Vamos a verlo con un ejemplo práctico. Imagina que quieres saber si los asistentes a un festival de música tienen más probabilidades de comprar merchandising oficial que los que no van.

Si después de analizar los datos, una calculadora de odds ratio te da un resultado de 4,5, la conclusión es directa y muy útil.

Las odds de que alguien compre merchandising son 4,5 veces mayores si ha ido al festival en comparación con alguien que no fue. Para los organizadores, este dato es oro puro, porque confirma que el evento es un motor de ventas potentísimo.

Aquí tienes una tabla para tener siempre a mano cómo interpretar los resultados:

Interpretación rápida de los valores del Odds Ratio (OR)

Una tabla de referencia para entender de un vistazo qué significa cada posible valor del odds ratio en un análisis.

Valor del Odds Ratio (OR)	Significado de la Asociación	Ejemplo práctico
OR > 1	Asociación positiva: El factor aumenta las probabilidades del resultado.	Un OR de 2 significa que el grupo expuesto tiene el doble de odds de experimentar el resultado.
OR = 1	Sin asociación: El factor no influye en las probabilidades del resultado.	Las odds son idénticas en el grupo expuesto y en el no expuesto.
OR < 1	Asociación negativa: El factor reduce las probabilidades del resultado (efecto protector).	Un OR de 0,5 significa que el grupo expuesto tiene la mitad de odds de experimentar el resultado.

Con esta guía, interpretar un odds ratio se vuelve mucho más sencillo, permitiéndote sacar conclusiones rápidas y fundamentadas a partir de tus datos.

El uso del odds ratio es muy habitual en estudios de salud. Por ejemplo, en investigaciones sobre la relación entre el tabaco y el cáncer de pulmón realizadas en España, se encontró que el odds ratio de desarrollar cáncer en fumadores era de aproximadamente 10,5 en comparación con no fumadores. Esto significa que los fumadores tienen más de 10 veces más probabilidades de desarrollar esta enfermedad, una cifra que demuestra una asociación extremadamente fuerte.

La fórmula del odds ratio, paso a paso

Si bien una calculadora de odds ratio te hace el trabajo sucio, entender de dónde sale la fórmula te da el control real. Créeme, desmontar las matemáticas que hay detrás es mucho más fácil de lo que parece. Todo empieza con una herramienta visual que es clave: la tabla de contingencia 2x2.

Esta tabla es la mejor forma de organizar los datos para que hablen por sí solos. Nos permite ver de un vistazo la relación entre estar expuesto a algo y que ocurra un resultado concreto.

La tabla de contingencia 2x2

Imagina que estamos investigando si una nueva crema hidratante (la exposición) de verdad ayuda a prevenir la piel seca (el resultado). La tabla 2x2 nos sirve para clasificar a todos los participantes en cuatro grupos muy claros.

Cada casilla de la tabla representa una combinación posible:

a: Usaron la crema y tienen la piel sana (el resultado esperado).
b: Usaron la crema pero no tienen la piel sana (tienen la piel seca).
c: No usaron la crema y, aun así, tienen la piel sana.
d: No usaron la crema y no tienen la piel sana (tienen la piel seca).

Esta estructura es el pilar de todo el cálculo. Es lo primero que tienes que montar antes de siquiera pensar en usar una calculadora de odds ratio.

La magia de la tabla 2x2 no está en contar por contar, sino en ordenar la información para que los patrones salgan a la luz. Es como un mapa que te lleva directo al cálculo del odds ratio.

Calculando las "odds" de cada grupo

Vale, ya tenemos los datos en su sitio. El siguiente paso es calcular las "odds" para cada grupo por separado. Olvídate de definiciones complejas: las "odds" no son más que la probabilidad de que algo pase dividida entre la probabilidad de que no pase.

Odds del grupo expuesto: Aquí simplemente dividimos los que tuvieron el resultado (casilla a) entre los que no lo tuvieron (casilla b). La fórmula es a / b.
Odds del grupo no expuesto: Hacemos lo mismo con el otro grupo. Dividimos los que tuvieron el resultado (casilla c) entre los que no lo tuvieron (casilla d). La fórmula es c / d.

Con estos dos numeritos ya sabemos qué probabilidades había de tener la piel sana dentro de cada grupo: el que usó la crema y el que no.

El siguiente diagrama te muestra cómo se conectan estos pasos, desde que recoges los datos hasta que tienes el resultado final en la mano.

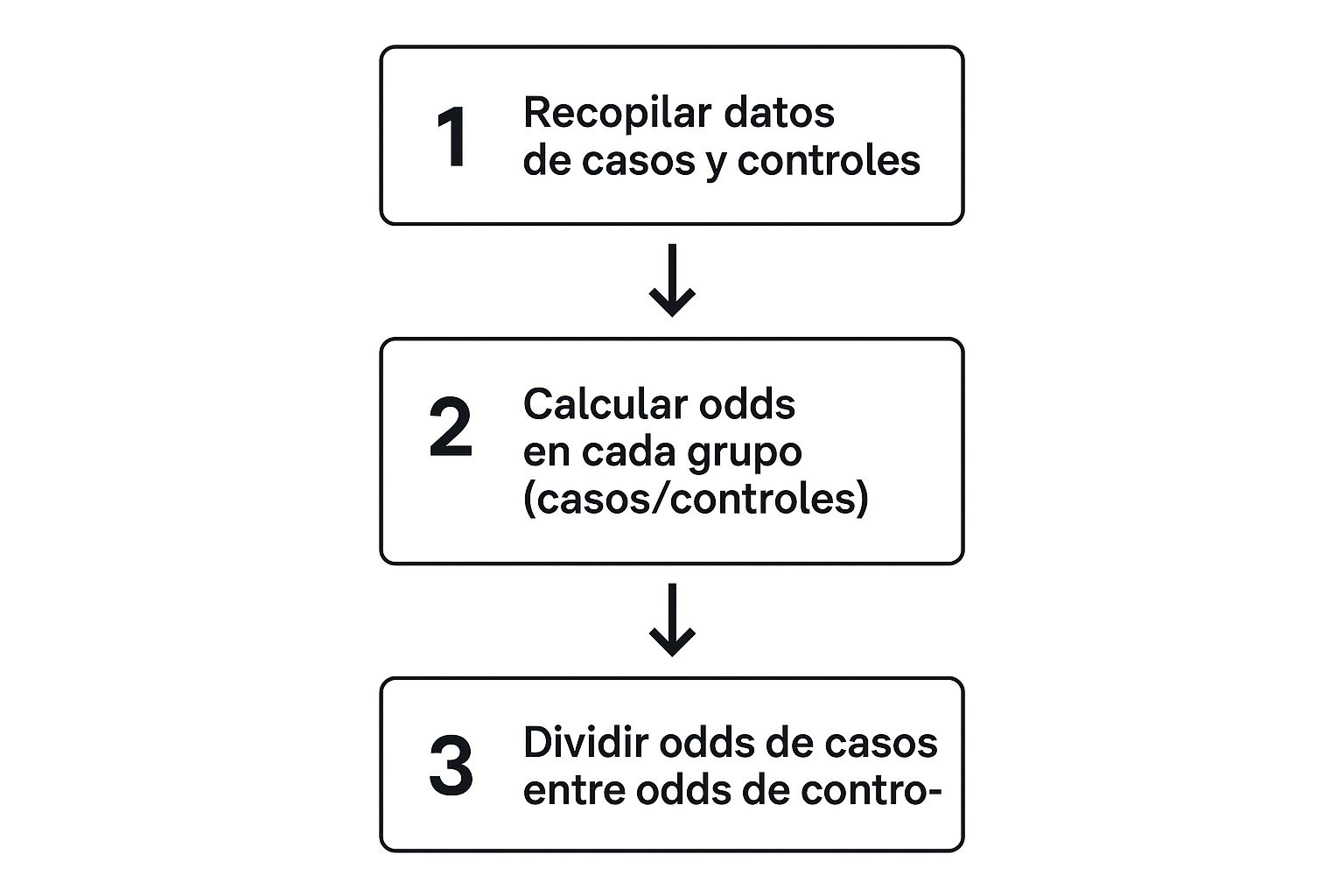
Como ves, el proceso deja claro que el odds ratio es, en esencia, una comparación directa entre las probabilidades de dos grupos.

La fórmula final del odds ratio

Ya casi estamos. Lo último que queda es comparar las odds de ambos grupos. ¿Cómo? Pues muy fácil: dividiendo las odds del grupo que usó la crema entre las odds del que no la usó.

La fórmula completa sería: OR = (a / b) / (c / d)

Por suerte, las matemáticas nos permiten simplificar esta expresión en algo mucho más fácil de recordar y de aplicar. Es la fórmula que usan todas las calculadoras:

OR = (a * d) / (b * c)

Esta fórmula cruzada (ad/bc) es el motor de cualquier calculadora de odds ratio. Multiplicas los números de las casillas diagonales y luego divides los resultados.

Pongamos un ejemplo: si a=50, b=10, c=20 y d=30, el cálculo sería (50 * 30) / (10 * 20) = 1500 / 200 = 7,5. Este 7,5 nos dice que las odds de tener la piel sana son 7,5 veces mayores si usas la crema.

Cuando entiendes este mecanismo, no solo sabes usar la herramienta, sino que puedes interpretar lo que te dice con total seguridad.

Cómo sacarle el máximo partido a una calculadora de odds ratio online

Saber cómo funciona la fórmula del odds ratio está muy bien para entender la base, pero seamos sinceros: en el día a día, lo que necesitas es rapidez y no cometer fallos. Aquí es donde una calculadora de odds ratio online se convierte en tu mejor aliada. Te quita de encima los cálculos manuales y te da los resultados al momento.

Estas herramientas están pensadas para que cualquiera pueda usarlas. Lo mejor es que se encargan ellas solas de la fórmula (ad)/(bc), así que tú puedes centrarte en lo que de verdad importa: interpretar los números y tomar decisiones con ellos. Solo necesitas tener a mano los cuatro valores de tu tabla 2x2.

Cómo introducir tus datos paso a paso

Verás que el proceso es de lo más simple. Si ya tienes tus datos organizados en la tabla, solo tienes que seguir estos pasos:

Ten claros tus cuatro valores: Asegúrate de saber qué número corresponde a cada casilla: a, b, c y d. Solo para refrescar la memoria:
- a: El grupo expuesto que presenta el resultado.
- b: El grupo expuesto que no presenta el resultado.
- c: El grupo no expuesto que presenta el resultado.
- d: El grupo no expuesto que no presenta el resultado.
Rellena las casillas: Las calculadoras suelen tener cuatro campos bien señalados. Simplemente, pon cada valor donde toca.
¡Dale a calcular!: Un clic y listo. La herramienta te dará el odds ratio al instante.

Aquí tienes un ejemplo típico de cómo se ve una de estas calculadoras. Como ves, solo tienes que introducir los datos para los que presentan el resultado ("Enfermo") y los que no ("Sano") en cada uno de los grupos.

Fíjate en la imagen. Después de meter los números, la herramienta no solo te da el odds ratio, sino también el intervalo de confianza, lo que te aporta una visión mucho más completa sobre la fiabilidad de tu resultado.

Ventajas que van más allá de la simple rapidez

Lo bueno de usar una calculadora de odds ratio no es solo que te ahorra tiempo. Su verdadero potencial está en la información extra que te proporciona, que es clave para hacer un análisis en condiciones.

Una de las métricas más valiosas que te dan estas herramientas es el intervalo de confianza del 95%. Este rango te dice lo preciso que es tu resultado. Si el intervalo no incluye el número 1, tienes un buen indicio de que la asociación que has encontrado es estadísticamente significativa.

Además de la precisión, estas calculadoras hacen que el análisis estadístico sea mucho más accesible, incluso si no eres un experto en la materia. Al final, lo que consigues es tener datos fiables en segundos, optimizando tu tiempo y mejorando la calidad de tus conclusiones.

Si te pica la curiosidad y quieres ver cómo se aplican las probabilidades en otros ámbitos, te puede interesar echar un vistazo a nuestro calculador de probabilidades.

Aplicaciones prácticas del odds ratio en el mundo real

El odds ratio no es solo una fórmula que se queda en los libros de estadística o en los laboratorios. Al contrario, es una herramienta súper práctica que nos ayuda a tomar mejores decisiones en un montón de campos diferentes, siempre basándonos en datos reales.

Su utilidad va mucho más allá de la medicina. Lo verás en marketing, en estudios sociales... En cualquier sitio donde necesites medir qué tan fuerte es la conexión entre dos cosas, el odds ratio te echa una mano para entenderlo mejor.

El odds ratio en el marketing y los negocios

Vamos a un caso práctico. Imagina que una tienda online lanza una nueva campaña de anuncios en redes sociales. El equipo de marketing se pregunta: ¿esto de verdad está funcionando para vender más? Para saberlo, comparan un grupo de usuarios que vieron el anuncio con otro que no lo vio.

Aquí es donde una calculadora de odds ratio entra en juego. Después de analizar los datos de compra, obtienen un resultado como este:

Odds Ratio = 2.8

¿Qué significa esto? Es muy sencillo y tremendamente útil. Las probabilidades (las odds) de que un cliente compre algo son 2,8 veces mayores si ha visto el anuncio. Con este numerito, el equipo puede justificar lo que gastaron en la campaña y planificar las siguientes con mucha más seguridad.

El odds ratio convierte las dudas en una ventaja. Permite que las empresas dejen de tomar decisiones a ciegas y empiecen a medir con claridad qué estrategias funcionan y cuáles no.

El odds ratio en la medicina y la salud pública

Este es, sin duda, el campo donde el odds ratio es más famoso y su impacto es enorme. Se usa a diario para entender factores de riesgo, comprobar si un tratamiento es eficaz o qué tan fiable es una prueba para diagnosticar una enfermedad.

Por ejemplo, su aplicación en el diagnóstico médico en España es clave. La odds ratio diagnóstica (ORD) se usa para medir la precisión de las pruebas médicas sin que la popularidad (o prevalencia) de la enfermedad influya en el resultado. En un estudio de 2021 en hospitales españoles, se vio que la ORD para un test rápido de COVID-19 era de unos 35. Esto quiere decir que la probabilidad de que la prueba diera positivo en una persona enferma era 35 veces mayor que en una persona sana. ¡Una fiabilidad altísima! Si quieres saber más, puedes profundizar sobre la odds ratio diagnóstica y su importancia.

Esta capacidad para ponerle un número a la eficacia de una prueba es fundamental para los médicos en su día a día.

El odds ratio en las ciencias sociales

En áreas como la sociología o la economía, el odds ratio es perfecto para desenredar relaciones complejas. Por ejemplo, un investigador quiere saber si tener un título universitario aumenta las posibilidades de encontrar un trabajo cualificado.

Para ello, analiza a dos grupos de personas: los que tienen estudios universitarios y los que no. Al meter los datos en una calculadora de odds ratio, el resultado podría ser este:

OR = 4.2: Las odds de conseguir un trabajo cualificado son 4,2 veces mayores para alguien con un título universitario.

Este tipo de análisis es oro puro para entender la desigualdad, el efecto de las políticas educativas o cómo se mueve el mercado laboral. Nos da números concretos para confirmar o descartar ideas sobre cómo funciona nuestra sociedad. Como ves, desde la efectividad de un anuncio hasta el valor de la educación, el odds ratio es una lente muy potente para entender las conexiones que dan forma a nuestro mundo.

Diferencias clave entre odds ratio y riesgo relativo

En el mundo de la estadística, una de las confusiones más típicas es la de mezclar el odds ratio (OR) con el riesgo relativo (RR). A simple vista, podrían parecer casi lo mismo, pero la realidad es que miden conceptos distintos. Saber cuándo usar cada uno es fundamental para no llegar a conclusiones equivocadas.

Piénsalo así: el riesgo relativo es mucho más directo, más intuitivo. Responde a una pregunta sencilla: "¿cuántas veces es más probable que algo suceda en un grupo en comparación con otro?". Por eso es la herramienta perfecta para estudios que siguen a la gente a lo largo del tiempo (los llamados estudios de cohorte).

El odds ratio, que ya hemos visto cómo se calcula, juega en otra liga. Su pregunta es un poco más retorcida: "¿cuánto mayores son las odds de haber estado expuesto en el grupo que sufrió el evento, frente al que no lo sufrió?". Suena a trabalenguas, pero es justo lo que necesitas para estudios que miran al pasado, como los de casos y controles.

La pregunta del millón: ¿cuándo usar cada uno?

Aquí está el quid de la cuestión: la elección entre OR y RR no es una preferencia personal, depende totalmente del diseño de tu investigación. No son intercambiables, y utilizar el incorrecto puede llevar a interpretaciones que se alejan mucho de la realidad.

Un detalle importante: cuando el evento que estudias es muy raro (una enfermedad con muy poca incidencia, por ejemplo), el valor del odds ratio se parece mucho al del riesgo relativo. Sin embargo, en cuanto el evento se vuelve más común, sus valores empiezan a separarse bastante.

Para que no te líes, aquí tienes una guía rápida:

Usa el Riesgo Relativo (RR) si tu estudio es prospectivo, es decir, de cohorte. Estás midiendo la aparición de un evento en dos grupos a lo largo del tiempo. Un ejemplo clásico sería seguir a un grupo de fumadores y a otro de no fumadores durante 10 años para ver cuántos desarrollan cierta enfermedad.
Usa el Odds Ratio (OR) si tu estudio es retrospectivo, o sea, de casos y controles. Aquí partes de un grupo que ya tiene una condición y otro que no, y miras hacia atrás para analizar si estuvieron expuestos a un factor de riesgo concreto.

Saber distinguir esto es tan crucial como entender bien las cuotas en las apuestas. De hecho, para los que les interese este mundillo, en nuestro blog tenemos una guía sobre cómo comprobar las apuestas de valor, un concepto que, en el fondo, también se basa en comparar probabilidades para tomar mejores decisiones.

Para tenerlo todo bien atado, he preparado una tabla que resume las diferencias clave de un solo vistazo.

Comparación directa Odds Ratio vs Riesgo Relativo

Aquí tienes un resumen de las diferencias fundamentales entre estas dos importantes medidas estadísticas para evitar confusiones comunes.

Característica	Odds Ratio (OR)	Riesgo Relativo (RR)
Pregunta que responde	Compara las odds de exposición entre casos y controles.	Compara la probabilidad de un evento entre expuestos y no expuestos.
Tipo de estudio ideal	Estudios de casos y controles (retrospectivos).	Estudios de cohorte (prospectivos).
Interpretación	"Las odds de exposición son X veces mayores..."	"El riesgo de que ocurra el evento es X veces mayor..."
Relación entre ambos	Tiende a sobrestimar el efecto cuando el evento es común.	Es una medida más directa y fácil de interpretar del riesgo.

Con esta tabla, queda claro que, aunque a veces se usen como sinónimos por error, cada indicador tiene su momento y su lugar. Dominar esta diferencia te permitirá analizar datos con mucha más precisión.

Entendiendo el odds ratio ajustado

A veces, una simple comparación entre dos variables no te cuenta toda la película. El mundo real es un lío de factores interconectados, y a menudo hay otros elementos, que llamamos variables de confusión, que pueden ensuciar la relación que de verdad nos interesa estudiar. Aquí es donde entra en juego un concepto un poco más avanzado, pero clave: el odds ratio ajustado.

Pongamos un ejemplo muy claro. Imagina que un estudio encuentra una conexión muy fuerte entre beber café y tener enfermedades de corazón. El odds ratio sale por las nubes. Pero, ¿y si resulta que muchos de los que toman café también fuman? En ese caso, el tabaco es una variable de confusión que podría ser la verdadera causa del problema, no el café.

El poder de aislar el efecto real

El odds ratio ajustado es la herramienta que nos permite "limpiar" esa interferencia. Piensa en él como una versión corregida del OR que tiene en cuenta el efecto de una o más de esas variables de confusión. El resultado es una visión mucho más nítida y precisa de la asociación que realmente importa.

Para calcularlo, ya no nos sirve una simple calculadora odds ratio de tabla 2x2. Necesitamos artillería estadística más pesada, y la más habitual es la regresión logística. Este modelo matemático es capaz de analizar un montón de variables a la vez y separar el impacto que tiene cada una de ellas por sí sola.

El odds ratio ajustado es como aplicar un filtro a una foto para eliminar el ruido. Te deja ver la imagen principal con total claridad, sin que otros elementos te distraigan de lo que de verdad estás analizando.

La regresión logística es una técnica muy extendida en España para calcular estos odds ratios ajustados en estudios clínicos. Por ejemplo, una investigación sobre enfermedad coronaria la utilizó para valorar a la vez factores de riesgo como la hipertensión, la diabetes y el tabaquismo. El modelo calculó un odds ratio combinado que señalaba que la probabilidad de sufrir la enfermedad subía hasta el 88,2% si todos estos factores estaban presentes, demostrando así la potencia del análisis ajustado. Si quieres profundizar, puedes explorar más sobre la versatilidad de la regresión logística en la investigación científica.

Entender bien este ajuste es fundamental para interpretar cualquier estudio serio, porque es la única forma de garantizar que las conclusiones son fiables y no están sesgadas por factores que se nos escapan a primera vista.

Preguntas frecuentes sobre el odds ratio

Siempre surgen algunas dudas cuando empezamos a usar una herramienta nueva. Vamos a aclarar las más habituales para que te muevas con total confianza al calcular e interpretar un odds ratio.

¿En qué tipo de estudios se usa más el odds ratio?

El odds ratio es el rey en los estudios de casos y controles. Piensa en ellos como una foto: comparas a un grupo que ya tiene una enfermedad o condición (casos) con otro que no la tiene (controles) para ver qué factores del pasado podrían estar asociados.

En cambio, para los estudios de cohorte, que son más como una película que sigue a la gente en el tiempo, lo más natural es usar el riesgo relativo (RR). Aun así, si el evento que estudias es raro (por ejemplo, una enfermedad poco común), el OR es una muy buena aproximación del RR.

¿Qué significa si el intervalo de confianza incluye el número 1?

Esta es una de las claves para interpretar tus resultados. Si el intervalo de confianza (el rango de valores probables para tu OR) contiene el 1, tu resultado no es estadísticamente significativo.

En palabras sencillas, quiere decir que no puedes descartar que la asociación que encontraste sea puro azar. Como el 1 significa "no hay asociación", si está dentro de tu rango de posibilidades, tienes que ser muy cauto y no puedes afirmar que existe una relación real.

¿Sirve una calculadora simple para un odds ratio ajustado?

No, para eso necesitas algo más potente. Una calculadora estándar de 2x2 es perfecta para un análisis simple, pero se queda corta cuando quieres "ajustar" o controlar el efecto de otras variables.

Para calcular un odds ratio ajustado, tendrás que recurrir a software estadístico más avanzado, como R o SPSS, que te permite hacer análisis de regresión logística y tener en cuenta múltiples factores a la vez.

Con las herramientas adecuadas, como la que encuentras en ArbiChat, puedes aplicar estos principios de probabilidad para tomar decisiones mucho más informadas y mejorar tus resultados. Puedes empezar a explorar cómo hacerlo en https://arbi.chat/es.